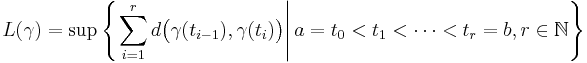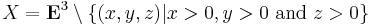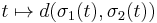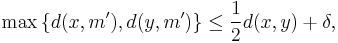CAT(k) space

In mathematics, a CAT(k) space is a specific type of metric space. Intuitively, triangles in a CAT(k) space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT(k) space, the curvature is bounded from above by k. A notable special case is k = 0: complete CAT(0) spaces are known as Hadamard spaces after the French mathematician Jacques Hadamard.

Originally, Alexandrov called these spaces "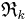 $\mathfrak{R}_k$ domain". The terminology "CAT(k)" was coined by Mikhail Gromov in 1987 and is an acronym for Élie Cartan, Aleksandr Danilovich Aleksandrov and Victor Andreevich Toponogov (although Toponogov was never doing curvature bounded above).

1 Definitions
2 Examples
3 Hadamard spaces
4 Properties of CAT(k) spaces
5 See also
6 References

Definitions

For a real number k, let M_k denote the unique simply connected surface (real 2-dimensional Riemannian manifold) with constant curvature k. Denote by D_k the diameter of M_k, which is +∞ if k ≤ 0 and π/√k for k > 0.

Let (X, d) be a geodesic metric space, i.e. a metric space for which every two points x, y ∈ X can be joined by a geodesic segment, an arc length parametrized continuous curve γ : [a, b] → X, γ(a) = x, γ(b) = y, whose length

$L(\gamma) = \sup \left\{ \left. \sum_{i = 1}^{r} d \big( \gamma(t_{i-1}), \gamma(t_{i}) \big) \right| a = t_{0} < t_{1} < \cdots < t_{r} = b, r\in \mathbb{N} \right\}$

is precisely d(x, y). Let Δ be a triangle in X with geodesic segments as its sides. Δ is said to satisfy the CAT(k) inequality if there is a comparison triangle Δ′ in the model space M_k, with sides of the same length as the sides of Δ, such that distances between points on Δ are less than or equal to the distances between corresponding points on Δ′.

The geodesic metric space (X, d) is said to be a CAT(k) space if every geodesic triangle Δ in X with perimeter less than 2D_k satisfies the CAT(k) inequality. A (not-necessarily-geodesic) metric space (X, d) is said to be a space with curvature ≤ k if every point of X has a geodesically convex CAT(k) neighbourhood. A space with curvature ≤ 0 may be said to have non-positive curvature.

Examples

Any CAT(k) space (X, d) is also a CAT(ℓ) space for all ℓ > k. In fact, the converse holds: if (X, d) is a CAT(ℓ) space for all ℓ > k, then it is a CAT(k) space.
n-dimensional Euclidean space Eⁿ with its usual metric is a CAT(0) space. More generally, any real inner product space (not necessarily complete) is a CAT(0) space; conversely, if a real normed vector space is a CAT(k) space for some real k, then it is an inner product space.
n-dimensional hyperbolic space Hⁿ with its usual metric is a CAT(−1) space, and hence a CAT(0) space as well.
The n-dimensional unit sphere Sⁿ is a CAT(1) space.
More generally, the standard space M_k is a CAT(k) space. So, for example, regardless of dimension, the sphere of radius r (and constant curvature 1/√r) is a CAT(1/√r) space. Note that the diameter of the sphere is πr (as measured on the surface of the sphere) not 2r (as measured by going through the centre of the sphere).
The punctured plane Π = E² \ {0} is not a CAT(0) space since it is not geodesically convex (for example, the points (0, 1) and (0, −1) cannot be joined by a geodesic in Π with arc length 2), but every point of Π does have a CAT(0) geodesically convex neighbourhood, so Π is a space of curvature ≤ 0.
The closed subspace X of E³ given by

$X = \mathbf{E}^{3} \setminus \{ (x, y, z) | x > 0, y > 0 \mbox{ and } z > 0 \}$

equipped with the induced length metric is not a CAT(k) space for any k.

Any product of CAT(0) spaces is CAT(0). (This does not hold for negative arguments.)

Hadamard spaces

Main article: Hadamard space

As a special case, a complete CAT(0) space is also known as a Hadamard space; this is by analogy with the situation for Hadamard manifolds. A Hadamard space is contractible (it has the homotopy type of a single point) and, between any two points of a Hadamard space, there is a unique geodesic segment connecting them. Most importantly, distance functions in Hadamard spaces are convex: if σ₁, σ₂ are two geodesics in X defined on the same interval of time I, then the function I → R given by

$t \mapsto d \big( \sigma_{1} (t), \sigma_{2} (t) \big)$

is convex in t.

Properties of CAT(k) spaces

Let (X, d) be a CAT(k) space. Then the following properties hold:

Given any two points x, y ∈ X (with d(x, y) < D_k if k > 0), there is a unique geodesic segment that joins x to y; moreover, this segment varies continuously as a function of its endpoints.

Every local geodesic in X with length at most D_k is a geodesic.

The d-balls in X of radius less than ½D_k are (geodesically) convex.

The d-balls in X of radius less than D_k are contractible.

Approximate mid-points are close to mid-points in the following sense: for every λ < D_k and every ε > 0, there exists a δ = δ(k, λ, ε) > 0 such that, if m is the mid-point of a geodesic segment from x to y with d(x, y) ≤ λ and

$\max \big\{ d(x, m'), d(y, m') \big\} \leq \frac1{2} d(x, y) %2B \delta,$

then d(m, m′) < ε.

It follows from these properties that, for k ≤ 0, the universal cover of every CAT(k) space is contractible; in particular, the higher homotopy groups of such a space are trivial. As the example of the n-sphere Sⁿ shows, there is, in general, no hope for a CAT(k) space to be contractible if k is strictly positive.

References

Alexander, S.; Kapovitch V., Petrunin A.. "Alexandrov Geometry, Chapter 7" (PDF). http://www.math.uiuc.edu/~sba/the-defs-CBA.pdf. Retrieved 2011-04-07.
Ballmann, Werner (1995). Lectures on spaces of nonpositive curvature. DMV Seminar 25. Basel: Birkhäuser Verlag. pp. viii+112. ISBN 3-7643-5242-6. MR 1377265.
Bridson, Martin R.; Haefliger, André (1999). Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 319. Berlin: Springer-Verlag. pp. xxii+643. ISBN 3-540-64324-9. MR 1744486.
Gromov, Mikhail (1987). "Hyperbolic groups". Essays in group theory. Math. Sci. Res. Inst. Publ. 8. New York: Springer. pp. 75–263. MR 919829.
Hindawi, Mohamad A. (2005). Asymptotic invariants of Hadamard manifolds. University of Pennsylvania: PhD thesis. http://www.math.upenn.edu/grad/dissertations/HindawiThesis.pdf.